Handbuch für die Modellierung von 3D Objekten - Teil 1: Grundlagen (Regeln für valide GML Geometrie-Elemente in CityGML)
Dokumentversionen
|
Version |
Datum |
Autor/en |
Status |
Bemerkungen |
|---|---|---|---|---|
|
0.1.0 |
01.10.2010 |
Coors |
nicht öffentlich |
Erstfassung |
|
0.2.0 |
14.10.2010 |
Coors |
nicht öffentlich |
Solid ergänzt |
|
0.3.0 |
23.10.2010 |
Gröger |
nicht öffentlich |
Verschmelzung mit Paper Gröger |
|
0.4.0 |
23.11.2010 |
Coors |
nicht öffentlich |
Redaktionelle Änderungen und Ergänzungen zu Planarität von Polygonen |
|
0.5.0 |
24.11.2010 |
Gröger |
nicht öffentlich |
Einarbeitung der Änderungen, die im CityGML-Forum von K.-H. Häfele vorgeschlagen wurden |
|
0.6.0 |
15.12.2010 |
Gröger |
öffentlich |
Einarbeitung der Anregungen von G. Juen |
|
0.7.0 |
20.01.2012 |
Häfele |
nicht öffentlich |
Konvertierung in Html, Verschiebung des Kapitel Planarität von Polygonen, Neues Kapitel CompositeSolid |
|
0.7.1 |
20.01.2012 |
Häfele |
nicht öffentlich |
Lizenzwechsel auf Creative Commons BY-NC-SA 4.0 |
Vorbemerkungen
- Die Regeln beziehen sich auf GML Version 3.1.
- Es wird davon ausgegangen, dass die Daten valide sind bzgl. des XML-Schemas von GML 3.1.
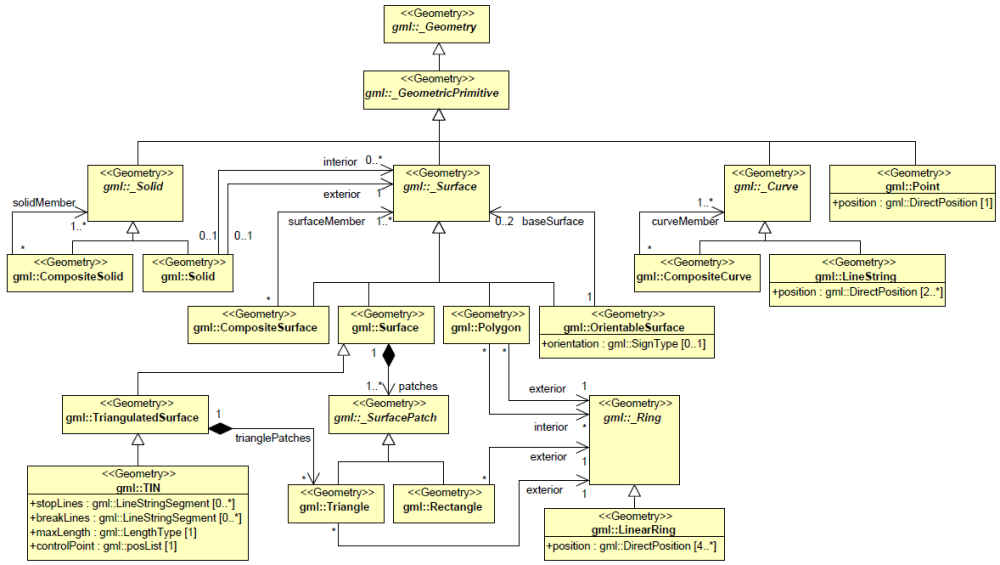
- Die Regeln sind eingeschränkt auf die Elemente von GML, die von CityGML genutzt werden (Profil von GML, siehe Abbildung 1 und Abbildung 2).
- Falls eine Bedingung nur für CityGML und nicht für GML im Allgemeinen gilt, so ist dies explizit vermerkt.
|
Abbildung 1: Profil von GML, das in CityGML verwendet wird (Primitive und Komposite) |
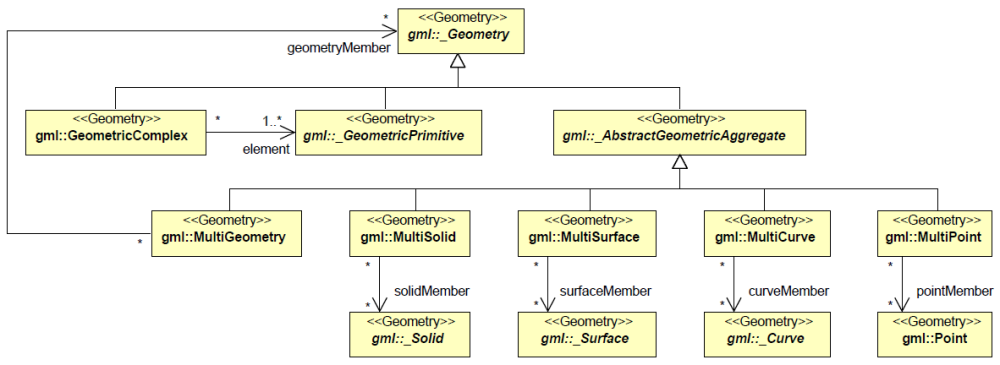
|
Abbildung 2: Profil von GML, das in CityGML verwendet wird (Komplexe und Aggregate) |
Spatial Reference Systems (SRS)
- Jedes Geometrie-Element (einschließlich pos, posList and coordinates) muss
- entweder im srsName-Attribut mit einem Wert belegt sein, oder
- den Wert des srsName-Attributs erben
- von seiner Elterngeometrie (auch rekursiv, von deren Elterngeometrie usw.) oder
- von der gml:Envelope (oder gml:Box), die der Wert der gml:boundedBy Property des Eltern-Features oder der Eltern-FeatureCollection ist (auch rekursiv).
- ein lokaler Wert des srsName Attribut geht dem geerbten Wert des srsName- Attributs vor
- sollte aus dem SRS nicht zweifelsfrei die Dimension erkennbar sein, muss das Attribut srsDimension bei Geometrieelementen (pos, posList) die Dimension des SRS enthalten
Definitionen
Geometrische Toleranzen
Planarität von Polygonen
Im CityGML müssen Polygone von einem planaren linearen Ring begrenzt sein . Aus praktischen Erwägungen werden auch Linear Ring Elemente, deren Punkte, die nicht exakt auf einer Ebene liegen sondern minimal davon abweichen, als planar akzeptiert. Intuitiv würde man fordern, dass ein Linearer Ring planar ist, wenn es eine Ebene E gibt, so dass die Distanz aller Punkte des Rings zu E einen gegebenen Grenzwert nicht überschreitet. Diese Ebene E kann über eine Ausgleichung aller Punkte aus R ermittelt werden, etwa durch Minimierung der maximalen Abstände von Punkten in R zu E (Ausgleichung gemäß Maximumsnorm) oder durch Minimierung der Quadrate der Abstände (Ausgleichung nach Gauß). Problematisch bei dieser Definition ist, dass auch minimale Knicke und Falten, wie in Abbildung 6 dargestellt, als planar akzeptiert werden. Dies entspricht aber in der Regel nicht dem intuitiven Verständnis einer planaren Fläche.
|
Abbildung 3: Minimale Knicke und Falten sollen auch bei nahezu planarenlinearen Ringen vermieden werden. |
|
Wenn solche Knicke und Falten erkannt werden sollen, muss das Kriterium zur Toleranz bei planaren linearen Ringen ergänzt werden. Es ergibt sich eine alternative Definition der Planarität Linearer Ringe:
Definition 1: Ein Linearer Ring heißt planar, wenn mindestens 3 Punkte des Rings nicht ko-linear sind und der Abstand der Punkte zu allen Ebenen , die durch 3 nicht ko-lineare Punkte , und aufgespannt werden, kleiner ist als eine gegebene Schranke :
Für die Überprüfung der Planarität wäre es wünschenswert, eine Vorgabe für die Schranke zu haben.
Da die Eigenschaft der Planarität invariant gegenüber Skalierungen sein sollte,
sollte in den Wert von die Ausdehnung bzw. Größe (Flächeninhalt, max. Punktabstand) des Linearen Ringes eingehen.
Dazu sollte die Punktgenauigkeit bekannt/festgelegt sein.
gml:posList
- Die Anzahl der Einträge in der Liste entspricht dem Produkt der Dimension des SRS und der Anzahl der direct positions.
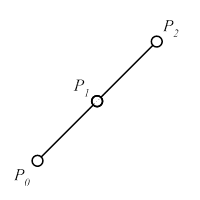
gml:_Curve, gml:LineString
- als _Curves sind nur gml:LineStrings erlaubt (gilt nur für CityGML)
- ein gml:LineString hat lineare Interpolation
- für die Kindelemente eines gml:LineString (Kontrollpunkte) gilt folgendes:
- diese bilden eine Folge von "pos" (DirectPositionType) oder "pointProperty" (PointPropertyType) Elementen. "pos"-Elemente sind Kontrollpunkte, die nur zu dieser Curve gehören. "pointProperty"-Elemente enthalten Punkte, die von anderen Geometrien referenziert werden können, oder referenzieren andere Punkte (über XLinks), die in anderen Geometrien definiert sind.
- Alternativ kann der gml:LineString aus einem "posList"-Element bestehen, das eine kompakte Möglichkeit der Angabe von Koordinaten bietet. In diesem Fall müssen alle Kontrollpunkte zu derselben Curve gehören und im selben SRS vorliegen. Die Anzahl der Punkte (Direct Position) ist mindestens zwei.
- Jeder Kontrollpunkt im gml:LineString erscheint nur einmal, außer dem ersten und letzten, die identisch sein können.
- Liniensegmente eines gml:LineString ergeben sich jeweils durch zwei aufeinanderfolgende Kontrollpunkte. Diese Liniensegmente dürfen sich nicht schneiden bzw. haben keine gemeinsamen Punkte. Ausgenommen sind Anfangs- und Endpunkt (definiert durch einen gemeinsamen Kontrollpunkt) zweier aufeinander folgender Liniensegmente.
gml:LinearRing
Der Linear Ring ist das grundlegende Element zur Geometriebeschreibung in CityGML. Jedes einzelne Polygon einer Gebäudegeometrie wird durch seinen Umring definiert. Eben dieser Umring wird durch das Element „Linear Ring“ beschrieben.
Zur formalen Definition des Linear Ring muss zunächst der Begriff der Sequenz eingeführt werden. Eine Sequenz ist eine geordnete Liste von Elementen. Im Gegensatz zu einer Menge ist die Reihenfolge der Elemente in einer Sequenz von Bedeutung. Ebenso kann in einer Sequenz ein Element mehrfach vorkommen. Eine endliche Sequenz mit Elementen wird durch die Elemente der Sequenz beschrieben: . Die leere Sequenz hat keine Elemente.
Eine endliche Sequenz von Punkten ist ein Linear Ring genau dann, wenn gilt:
(i) Der erste und der letzte Punkt der Sequenz sind identisch: (closeness)
(ii) Mit Ausnahme des ersten und letzten Punktes sind alle Punkte verschieden, d.h.
Formelschreibweise überprüfen
(iii) Zwei Kanten und mit dürfen sich nur in einem Start-/ Endpunkt berühren. Weitere Schnitt- bzw. Berührungspunkte sind nicht zulässig (no self intersection).
Sind alle Punkte der Sequenz ko-planar, wird der Linear Ring planar genannt.
Beispiel:
|
mit
|
<gml:LinearRing> <gml:pos> 1 1 1 </gml:pos> <gml:pos> 3 1 1 </gml:pos> <gml:pos> 3 3 1 </gml:pos> <gml:pos> 1 3 1 </gml:pos> <gml:pos> 1 1 1 </gml:pos> </gml:LinearRing> |
|
|
Abbildung 4: Planarer Linear Ring nach Definition, in GML und als graphische Darstellung |
||
Hinweis:
Die beiden linearen Ringe und sind nicht identisch.
gml:Polygon
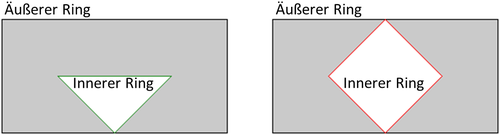
- Ein planarer linearer Ring definiert den Rand eines Polygons (äußerer Ring).
- Ein Polygon ist durch genau einen solchen äußeren Ring und innere Ringe definiert. Jeder innere lineare Ring muss ebenfalls planar sein, und der äußere und alle inneren linearen Ringe müssen in derselben Ebene (im Rahmen einer gegebenen Toleranz) liegen.
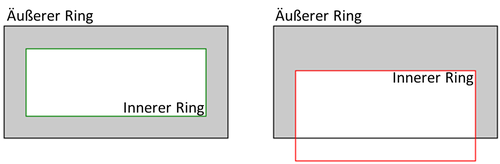
- Jeder innere lineare Ring muss innerhalb des Gebiets der Ebene liegen, das der äußere Ring begrenzt.
| Abbildung 5: Polygon mit korrektem inneren Ring (links) und nicht korrektem inneren Ring (rechts) |
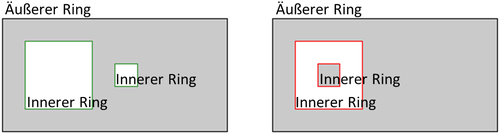
- Die inneren linearen Ringe dürfen nicht verschachtelt sein, d.h. kein innerer Ring liegt in dem Gebiet der Ebene, das ein anderer innerer Ring definiert.
| Abbildung 5: Polygon mit zwei korrekten inneren Ringen (links) und zwei verschachtelten, nicht korrekten inneren Ringen (rechts) |
- Die inneren Ringe und der äußere Ring dürfen sich paarweise in endlich !!!!! (evtl. nur einer) vielen Punkten berühren. Dabei muss das Innere des Polygons zusammenhängend sein.
| Abbildung 5: Polygon mit korrektem, innerem Ring, der den außeren Ring an einem Punkt berührt (links) und nicht korrektem innerem Ring, der den äußeren Ring an zwei Punkten berührt und damit dass Polygon spaltet (rechts) |
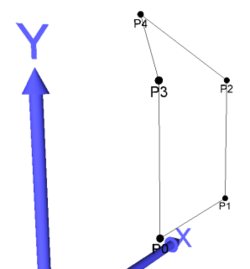
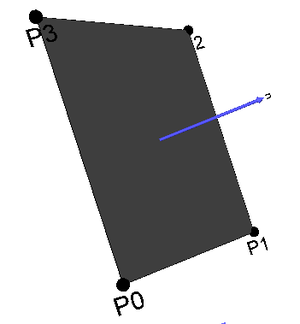
- Die Reihenfolge der Punkte des äußeren Linear Rings definiert die Orientierung des Polygons. In existieren mindestens drei nicht ko-lineare Punkte , und , die eine Ebene aufspannen. Der Vektor , der sich aus dem normalisieren Kreuzprodukt der beiden Vektoren und ergibt, wird als Flächennormale des Polygons bezeichnet:
Bemerkung: Aufgrund der Toleranz planarer linearer Ringe ist die Flächennormale des Polygons nicht eindeutig bestimmt.
Hinweis: Die beiden von den linearen Ringen und definierten Polygone haben dieselbe geometrische Ausprägung, unterscheiden sich aber hinsichtlich der Orientierung.
| Abbildung 5: Polygon mit Flächennormale n |
gml:OrientableSurface
- Hat das Attribut “orientation” den Wert "+", so ist die OrientableSurface identisch zu der baseSurface. Ist der Wert der Orientierung "-", dann entspricht die OrientableSurface einer Surface mit einer Normalen, die der Normalen der baseSurface entgegen gesetzt gerichtet ist. "+" ist der Default-Wert des Attributs “orientation”.
- Entweder referenziert das Element “baseSurface” die base surface durch ein XLink-Attribut, oder das Element “baseSurface” enthält die base surface als Kindelement. Die base surface hat eine positive Orientierung.
gml:MultiSurface
Eine Menge von Polygonen wird als MultiSurface bezeichnet. Es gelten keinerlei Bedingungen für die Struktur der in enthaltenen Polygone. Sie können sich beispielsweise überlappen oder durchdringen. Es ist auch nicht notwendig, dass die Polygone in eine zusammenhängende Oberfläche beschreiben. Die Polygone können beliebig orientiert sein.
Das MultiSurface-Element ist daher sehr einfach zu nutzen.
Allerdings sind die häufigsten Fehler, die in einem Modell enthalten sind, auf die Verwendung von MultiSurface-Elemente zurückzuführen, da keinerlei strukturgebende Randbedingungen vorhanden sind.
In der Computergraphik wird eine solche Menge von Polygonen ohne explizite Struktur auch „Polygon-Suppe“ genannt.
Problematisch ist bei der Verwendung von MultiSurface Elementen, dass mit diesem Geometrieelement Objekte dargestellt werden können, die keine Festkörper sind. Dies ist zwar ein sehr flexibler Ansatz, sollte aber nur verwendet werden, wenn explizit keine Festkörper modelliert werden sollen.
|
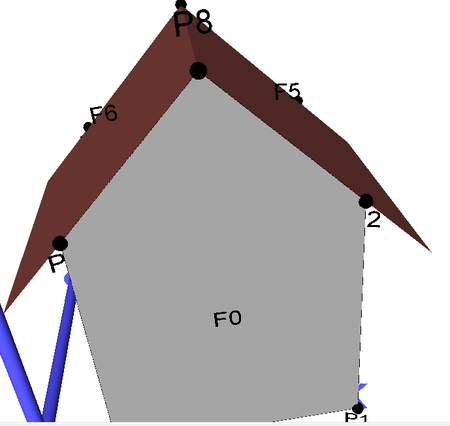
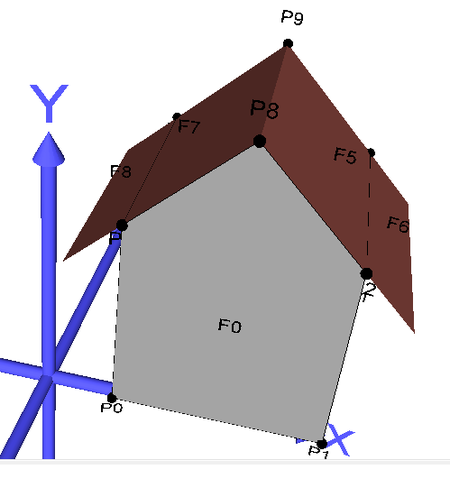
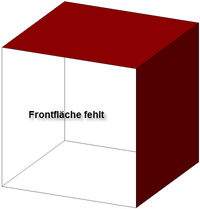
Abbildung 6: Modellierung von Dachüberständen als einfache Polygone. Im linken Modell wird das Gebäude mit einer MultiSurface-Geometrie beschrieben, die aus 7 Polygonen besteht. Eine Volumenberechnung ist nicht möglich, da es sich um keinen geschlossen Körper handelt. Die rechte Abbildung zeigt dasselbe Modell, nun durch eine Solid (Gebäude) und eine zusätzliche MultiSurface-Geometrie (2 Polygone für Dachüberstand) beschrieben (vgl. CityGML Standard v1.0, S.61). Diese Variante ist zu empfehlen. |
|
gml:CompositeSurface
Eine CompositeSurface ist eine Menge von Polygonen, für die folgendes gilt:
- Die Schnittmenge zweier Polygone und aus ist entweder leer oder besteht nur aus Punkten und/oder Kanten, die auch in den beiden linearen Ringen vorkommen. Bezeichne den planaren linearen Ring, der das Polygon definiert. Dann gilt:
- Jede Kante eines linearen Rings , der ein Polygon definiert, wird höchstens einmal als Kante in einem linearen Ring genutzt, der ein anderes Polygon definiert.
Es gilt und . - Die Polygone aus sind so orientiert, dass die Flächennormale benachbarte Polygone in dieselbe Richtung zeigen.
- Die Vereinigung aller Polygone aus ohne die Kanten oder Punkte, in denen sich die Polygone berühren, ist isomorph zu einem Polygon.
Aus (1) und (2) ergibt sich, dass die Oberfläche, die durch beschrieben wird, keine sich gegenseitig überlappenden oder durchdringenden Polygone enthalten darf (Polygone berühren sich höchstens in Punkten oder Kanten).
gml:Solid
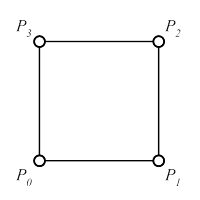
Ein Solid modelliert einen beliebigen Festkörper. Die Oberfläche des Solid wird über eine Menge von Polygonen beschrieben, die bestimmte strukturgebende Eigenschaften erfüllen müssen. Die Menge von Polygonen beschreibt die Oberfläche eines Solid genau dann, wenn gilt:
- Die Schnittmenge zweier Polygone und aus ist entweder leer oder besteht nur aus Punkten und Kanten, die auch in den beiden linearen Ringen vorkommen. Bezeichne den planaren linearen Ring, der das Polygon definiert. Dann gilt:
- Jede Kante eines linearen Rings , der ein Polygon definiert, wird genau einmal als Kante in einem linearen Ring genutzt, der ein anderes Polygon definiert.
Es gilt und . - Die Polygone aus sind so orientiert, dass die Flächennormalen nicht ins Innere des Festkörpers zeigen, sondern nach außen.
- Die Polygone aus sind zusammenhängend, d.h. in dem dualen Graphen von gibt es einen Weg, der alle Knoten umfasst. Der duale Graph GC =(VC, EC) von besteht aus einer Menge VC von Knoten und einer Menge EC von Kanten. Jeder Knoten v aus VC repräsentiert genau ein Polygon aus . Eine Kante zweier Polygone und aus wird in GC durch eine Kante in EC dargestellt.
- Für jeden Punkt , der in einem linearen Ring eines Polygons aus vorkommt, gilt: Der Graph , der aus Polygonen und Kanten gebildet wird, die berühren, ist zusammenhängend. Dabei repräsentiert jeder Knoten aus genau ein Polygon, dessen linearer Ring enthält. Zwei Knoten sind genau dann mit einer Kante aus verbunden, wenn die Polygone, die durch die Knoten repräsentiert werden, eine gemeinsame Kante haben, die berührt .
Aus (1) und (2) ergibt sich, dass die Oberfläche, die durch beschrieben wird, keine Löcher enthalten darf. Mit den weiteren Bedingungen (4) und (5) ergibt sich, dass das Innere des durch beschriebenen Festkörpers zusammenhängend sein muss. wird auch als geschlossene CompositeSurface bezeichnet.
Beispiele:
|
Korrekt: 6 Flächen, geschlossen, Flächenorientierung korrekt |
Korrekt: 11 Flächen, geschlossen, Flächenorientierung korrekt |
Korrekt: 10 Flächen, geschlossen, Flächenorientierung korrekt |
Korrekt: 30 Flächen, geschlossen, Flächenorientierung korrekt |
|
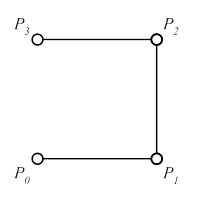
Nicht Korrekt: 5 Flächen, nicht geschlossen, Flächenorientierung korrekt |
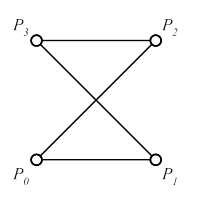
Nicht Korrekt: 6 Flächen, geschlossen, Flächenorientierung nicht korrekt |
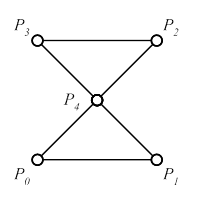
Nicht Korrekt: 12 Flächen, nicht geschlossen (zwei Außenhüllen), Flächenorientierung korrekt |
Nicht Korrekt: 12 Flächen, nicht geschlossen (innere und äußere Hülle), Flächenorientierung korrekt |
gml:CompositeSolid
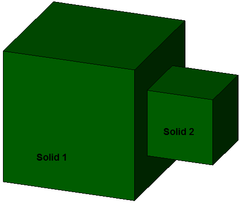
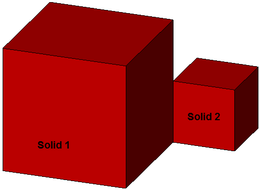
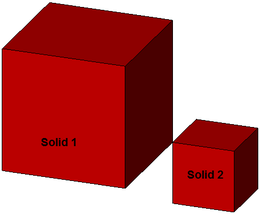
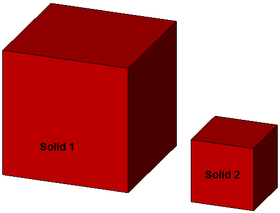
Ein CompositeSolid wird durch eine nichtleere Menge von Solids (vgl. 12.) beschrieben, für die gilt:
- Der Schnitt der Inneren zweier Solids , , 1 ≤ i ≤ n, 1 ≤ j ≤ n, i ≠ j, ist leer, d.h. entweder sind beide Solids , disjunkt oder beide berühren sich nur in Flächen, Linien oder Punkten
- Sei die Vereinigung aller Solids aus . Dann ist die Begrenzung von (die Oberfläche von ohne die Flächen oder Punkte, in denen sich die Solids berühren) die Begrenzung eines Solid.
In CityGML werden bei CompositeSolids ebenso wie bei Solids innere Einschlüsse (Hohlräume) nicht betrachtet.
Beispiele:
|
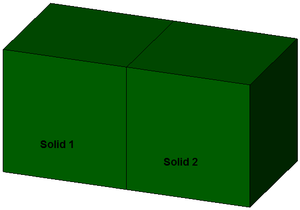
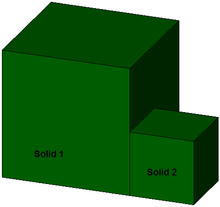
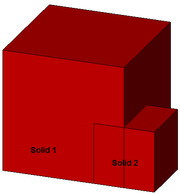
Korrekt; Flächenberührung |
Korrekt; Flächenberührung |
Korrekt; Flächenberührung |
Korrekt; Flächenberührung |
|
Falsch; Linienberührung |
Falsch; Punktberührung |
Falsch; keine Berührung |
Falsch; Durchdringung |
|
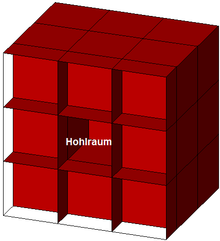
Falsch; 26 Quader mit Flächenberührung |
aber mit Hohlraum |
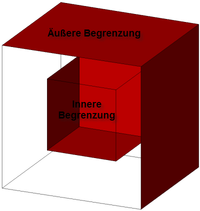
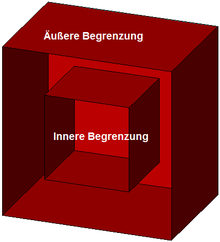
nicht korrekt; Innere Begrenzung |
gml:Triangle
- Ein Triangle ist ein Spezialfall eines Polygons, das von einem äußeren linearen Ring mit vier Punkten begrenzt wird.
- Es gibt keine inneren Ringe (kein Element "interior").
gml:TriangulatedSurface
Eine triangulated surface ist eine Composite Surface (vgl. Abschnitt 10), die nur aus triangles besteht, jedoch nicht geschossen ist, d.h. sie darf Ränder besitzen. Bezüglich der Art und Weise, wie die Triangulation hergeleitet wurde, gibt es keine Einschränkung.
gml:Tin
Im Gegensatz zur gml:TriangulatedSurface sind in einem gml:Tin die triangles nicht explizit repräsentiert, sondern nur durch ihre Eckpunkte (genannt Kontrollpunkte). Zusätzlich können breaklines, stop lines und die maximale Länge einer Dreiecksseite in einem gml:Tin repräsentiert werden.
- Ein TIN ist eine triangulierte Oberfläche, die Ergebnis der Anwendung eines Delaunay Algorithmus oder eines ähnlichen Verfahrenes ist. Diese wird ergänzt um die Berücksichtigung von Stoplinien, Bruchkanten und der max. Länge von Dreieckseiten. Diese Netze erfüllen das Delaunay Kriterium:
- Für jedes Dreieck im TIN enthält der Kreis, der durch die drei Punkte des Dreiecks definiert ist, keinen weiteren Eckpunkt eines anderen Dreiecks.
- Stoplinien sind Linien, an denen die lokale Kontinuität und Regularität der Oberfläche zweifelhaft ist. In diesen pathologischen Gebieten sollen Dreiecke, die von Stoplinien geschnitten werden, entfernt werden. Dabei können Löcher in der Oberfläche entstehen. Werden Dreiecke am Rand der Oberfläche entfernt, ergibt sich eine Veränderung des Randes der Oberfläche.
- Bruchkanten (Breaklines) sind Linien, an denen sich die Gestalt der Oberfläche signifikant ändert (Grate, Tallinien, ...). Solche Segmente sollen im TIN enthalten sein, auch wenn diese das Delaunay-Kriterium verletzen.
- Max. Länge von Dreiecksseiten: Gebiete der Oberfläche, in denen die Datendichte für eine angemessene Ermittlung der Oberfläche nicht ausreichend ist, werden durch Angabe eines Kriteriums entfernt. Dieses Kriterium bezieht sich auf die Länge der Dreiecksseiten. Alle Dreiecke, deren Seiten (mind. eine) diese Länge überschreiten, werden aus der Oberfläche entfernt.
- Es gibt mindestens drei Kontrollpunkte.
- Die Oberfläche, die durch das TIN repräsentiert ist, hängt nicht von der Reihenfolge der Kontrollpunkte ab. Anwendungsschemata können Angaben zur Reihenfolge der Kontrollpunkte beinhalten, um die Rekonstruktion des TIN aus den Kontrollpunkten zu beschleunigen.